Operations with functions

We define the addition, subtraction, multiplication and division of functions as:

· (f ± g)(x) = f(x) ± g(x)

· (f · g)(x) = f(x) · g(x)

· (f/g) (x) = f(x)/g(x)     (if g(x)≠0)

Example: if f(x) = x² -2 and g(x) = 3x + 2, then:

(f + g)(x) = f(x) + g(x) = x² + 3x

(f - g)(x) = f(x) - g(x) = x² – 3x - 4

(f · g)(x) = f(x) · g(x) = 3x³ + 2x² – 6x - 4

(f/g) (x) = f(x)/g(x) = (x^₂ -2)/(3x + 2),  if x ≠ -2/3

Function composition is the application of one function to the results of another. It is represented by g_°f, and we say “f composed with g”.
    g_°f(x) = g(f(x))   (if f(x) € Dom g)
    

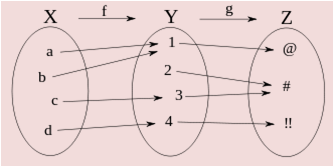
Example: if  f(x) = x + 1; g(x) = x², then:
    

 g_°f(x) = g(f(x)) = g(x + 1) = (x + 1)² = x² + 2x +1

 f_°g(x) = f(g(x)) = f(x2) = x² + 1

NOTE: As you can see, the function composition doesn’t follow the commutative property:   
            g_°f ≠ f_°g

An inverse function of f is a function that undoes another function, that is, it is a function f^-1 such that   

f_° f^-1(x) = f^-1 _°f (x) = i(x) = x

Example 1: if  f(x) = x², then f^-1(x) = √x, because

    f_° f^-1(x) = f(√x) = (√x)²= x

    f^-1 _°f (x) = f^-1(x²) = √x² = x

Example 2: if  f(x) = 1/x, then f^-1(x) = 1/x, because

    f_° f^-1(x) = f(1/x) = 1/(1/x)= x

    f^-1 _°f (x) = f^-1(1/x) = 1/(1/x)= x

Example 3: find the inverse function of f(x) = √(2x)

    x = √(2y) → x² = 2y → y = f^-1(x) = x²/2

NOTE: inverse functions are symmetric and their axis of symmetry is the line: y = x

 

 

Exercises:

1.- Let f(x) = x² + 2 and g(x) = x - 2. Calculate:

a) (f + g)(x)

b) (f - g)(x)

c) (f · g)(x)

d) (f/g)(x)

e) (g º f)(x)

f) (f º g)(x)

 

2.- Find out the inverse function of these functions:

a) f(x) = x² - 7

b)  

 

 

 

Solutions:

1.- a) y = x² + x; b) y = x² - x +4; c) y = x³ - 2x² + 2x - 4; d) y = (x² + 2)/(x -2); e) y = x²; f) y = x² - 4x + 6

2.- a) y = √(x+7); b) y = (-7x)/(x-3)