Functions
A function f, is a relation between two sets with the property that each element in the first set is related to exactly one element in the second set.
f: X →Y, X is the initial set and Y the final set (codomain)
x →y = f(x) x is called independent variable (variable) and y is called dependent variable. f(x) is the image of x under f.
Example 1: the function that associates each student of this class with his or her age.
Example 2: the function that associates each natural number with its double.
There are 4 ways to express a function:
- Verbal way, as in the examples above.
- Algebraic way, with a formula. In the example 2: y = f(x) = 2x
- With a table:

- With a graph:

The domain of a function is the subset of the initial set of the elements that have an image.
The range or image is the subset of the codomain of the elements that are images of an element of the domain.
Example 1: the initial set and the domain is the class, the codomain is the natural numbers and the range = {15, 16, 17}.
Example 2: the initial set and the domain is N and the range is the set of even numbers.
Example 3:
it is not a function
Example 4:
Domain = R
Range = [-3,3]
Example 5: Whole number portion function
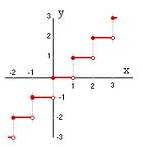
Domain = R Range = Z
Exercises:
1.- Decide if the following relations are functions or not, and if they are, find their domain and range:
a) 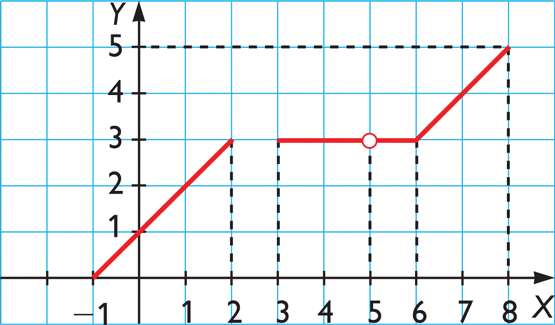
b) 
c) 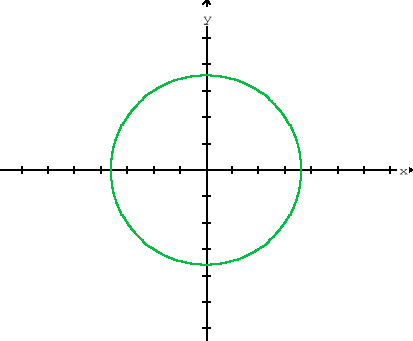
Solutions:
a) it's a function, dom = [-1,2]U[3,5)U(5,8], range = [0,5]
b) it's a function, dom = range = R
c) it is not a function
2.- True-False Question
Decide if the following relations are functions:
Retroalimentación
Falso
Retroalimentación
Falso
Retroalimentación
Verdadero
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 3.0