4. symmetry
A function is even if f(-x) = f(x), that is, if its graph is symmetric with respect to y-axis:
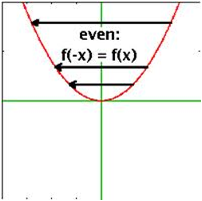
A function is odd if f(-x) = -f(x), that is, if its graph shows rotational symmetry with respect to the origin:
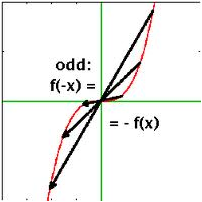
Example 1: f(x) = x4 - x2 is an even function because f(-x) = (-x)4 – (-x)2 = x4 – x2 = f(x)
Example 2: f(x) = x3 is an odd function because f(-x) = (-x)3 = - x3 = -f(x)
Example 3: f(x) = x3 – 3 is neither an even function nor an odd function because:
f(-x) = (-x)3 - 3 = -x3 – 3 ≠ -f(x)
Exercise: study the symmetry of these functions:
a) f(x) = x4 + 3x2 - 7
b) f(x) = x5 - x3 + x - 7
c) ![]()
Solutions: a) it is an even function: b) it is neither an even nor an odd function; c) it is an odd function
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 3.0